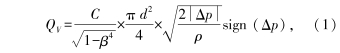摘要(yào):爲了研究孔闆流(liu)量計
在動态非穩(wěn)定流态或振蕩流(liú)态下的瞬時壓力(li)-流量特性,理論分(fen)析了孔闆前後的(de)旋渦城大小随流(liú)速變♻️化是引起孔(kong)闆進出口瞬時流(liu)量差的主要原因(yīn).借助CFD數值解析方(fāng)法📱,建立孔闆模型(xíng),并在模型入口加(jiā)載某⭕一頻率下的(de)正弦流速,對孔闆(pan)❤️流量計在🚶振蕩流(liu)态下的瞬時壓力(lì)-流量特性進行分(fèn)析.結果🤞表明:當孔(kǒng)闆流量計處于低(di)頻振蕩流動狀态(tài)時,孔闆兩端差壓(yā)也處🙇♀️于周期✍️振蕩(dang)狀态,差壓與節流(liú)孔瞬時流量同頻(pín)不同相,差壓幅值(zhí)随入口流速振幅(fu)增大而線🌂性增大(da),且線性增長♻️系數(shu)與振蕩頻率相關(guan);孔闆的入口與出(chu)口存在周期波動(dong)的瞬時流量⛷️差,振(zhen)蕩頻率越大或入(rù)口流速峰值越小(xiao),瞬時流量🧑🏽🤝🧑🏻差的波(bō)動越小,由于相位(wèi)滞後和瞬時流量(liàng)差的存🌈在,使孔闆(pan)流量計的測量流(liú)量與實際出口流(liú)量之🐪間存在偏差(cha).振蕩頻率越大,偏(piān)差也❌越大.
孔闆流(liu)量計因其結構簡(jian)單、耐用而成爲目(mù)前國際🌂上💃标準化(hua)程度最高、應用最(zui)爲廣泛的一種流(liu)量計,因此研究節(jiē)流孔的流量特性(xing),對提高孔闆流量(liang)計測量不确定度(du)的認識具有很重(zhòng)要的意義.孔闆流(liú)🐆量計通過測量壓(ya)差進而獲得流量(liang).當液流經過節🧡流(liu)孔,流束縮小,流速(su)變大并伴随着較(jiao)大的壓力降.流束(shu)的最小💋橫斷面出(chū)現在實💘際縮口的(de)下遊,稱爲縮流斷(duàn)面❌.在縮流斷面處(chu),壓力最低.壓降的(de)産生是由于在孔(kǒng)闆的兩側🏒側面出(chū)現回流區及旋渦(wo)域,造成較大的🤞内(nèi)部紊流和能量損(sǔn)耗的結果[1-2].旋渦域(yu)的🌍大小取決于流(liú)動雷諾數,随着雷(léi)諾數的🐪增大,渦旋(xuan)㊙️強度增加[3].
流體力(lì)學中對孔口恒定(dìng)出流的描述爲孔(kǒng)闆結構的🙇🏻設計提(ti)供了理論依據.但(dàn)實際應用中,由于(yú)外界🔱激勵引起❌的(de)壓力波動,圓💃管内(nei)流體常處于動态(tài)非穩定流态或振(zhen)蕩流态[4],孔闆流👅量(liang)計内🌈部流場結構(gòu)變化極爲複雜,因(yin)此,計量孔闆的瞬(shùn)時流量特性往往(wang)與理論分析結果(guǒ)存在偏差因此,有(you)必要對孔闆在非(fei)穩定流态下的流(liu)量特性進行研究(jiū).
通過Fluent流體仿真程(cheng)序,對不同節流孔(kǒng)直徑比的孔闆☔,以(yi)水爲介質在振蕩(dang)流态下的流動過(guo)程進行仿真,對其(qí)❄️瞬時🌍壓力-流量☁️特(te)性⛷️進行分析.
1理論(lun)分析
通常在特定(dìng)測壓位置和特定(dìng)流體參數情況下(xià),根據流💋體🌈流動的(de)連續性方程和伯(bo)努利方程可推導(dao)🛀出孔闆前後差📧壓(ya)△p與流經節流孔的(de)體積流量QY滿足以(yǐ)下函數關系♉[5],即
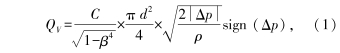
式(shì)中:C爲流出系數;ρ爲(wèi)流體密度;β爲節流(liu)孔的直徑比(β爲節(jiē)🔆流孔直㊙️徑d與圓管(guan)内徑D的比值,即β=d/D);sign爲(wèi)符号函數*.
圓管進(jin)口流量可計算公(gong)式爲
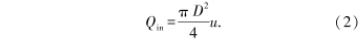
孔闆流量計(jì)通過測量節流孔(kǒng)兩端差壓進而獲(huò)得節流孔流👄量✔️QV.對(dui)于不可壓縮的定(dìng)常流,圓管進口流(liú)✌️量Qin和出口流量Qout與(yǔ)節流孔流量QY相等(deng),聯立以上方程可(ke)得節流孔兩㊙️端差(cha)壓與人口流速的(de)關系表達式爲

由(yóu)式(3)可知,孔闆兩端(duān)差壓也呈周期性(xìng)波動,.其振蕩🧑🏽🤝🧑🏻頻率(lü)與孔闆人口流速(sù)振蕩頻率相同.
孔(kong)闆前後存在旋渦(wō)域.旋渦域的大小(xiao)占據圓管空間,液(ye)體🙇🏻在旋渦域停留(liú),不流向下遊管道(dào).旋渦域增✌️大,則💜流(liú)向圓管出口的液(yè)流減少.由于孔闆(pǎn)前後遊渦旋強度(du)随流動雷諾數增(zēng)大而增大🚶,即随流(liú)速增加旋渦域變(biàn)大3],.在振🆚蕩流态下(xià),旋渦域大小随入(ru)口流速變化也🌈表(biǎo)現爲周期性變化(huà)狀态,變化頻率與(yu)流速振蕩頻率相(xiang)同.因此,在某一極(ji)短時間段内,旋渦(wō)域的體積變化量(liang)表現爲圓管進、出(chū)口的瞬時流量🥵之(zhī)差.對于不可壓縮(suō)的非定常流,人口(kou)瞬時流量Qin與出口(kou)瞬🚶♀️時流量Qout和節流(liú)孔瞬🌈時流量QY滿足(zu)以下關系,即

式中(zhōng):△Q表示圓管進出口(kǒu)瞬時流量差.瞬時(shí)流量差的🚩存在,使(shi)孔闆流量計實際(jì)測量流量Qv與出口(kǒu)瞬時流量Qout之間不(bú)❤️可避免存在偏差(chà).
事實上,由于節流(liu)孔的壓降作用,當(dāng)孔闆下遊壓力低(di)🐉于液體🤩飽和蒸氣(qi)壓以下,氣泡将在(zai)下遊管道産生,形(xing)成閃蒸現象.當壓(ya)力上升,氣泡破裂(liè)瞬間産生局部空(kong)穴,高壓液體重新(xin)流向這些空間.顯(xian)然,氣泡和空穴占(zhan)據了下遊管道空(kong)間,使進、出口流
量(liàng)Qm與Qout,存在差異,出現(xiàn)瞬時流量差實際(jì)孔闆流量計使用(yong)過🌈程中避免閃蒸(zhēng)和空穴現象的出(chū)現,故文中對其影(yǐng)響不做表述.
爲進(jin)一步探究孔闆的(de)瞬時壓力流量特(te)性,文中以上述理(lǐ)論分析爲基礎,結(jié)合有限元分析思(sī)想,對孔闆流量計(ji)在低🔴頻微幅振蕩(dàng)流态下的壓力流(liu)量特性進行了分(fen)析🆚.
2期修仿真
2.1控基(jī)文圖
文中選用RNGk-ε湍(tuān)流模型對孔闆的(de)流量特性進行模(mó)拟.該模型的控制(zhi)方程分别爲連續(xù)性方程

上述式中(zhong):xi,xj分别爲縱向和橫(héng)向坐标;ui,uj分别爲縱(zòng)向和想✊象🌈的速度(dù)分量;p爲流體壓力(li);v爲流體運動黏度(dù);vt爲流體渦流黏度(dù),vt=Cμk²/Ɛ,其中🈲k爲湍動能,Ɛ爲(wèi)湍動耗散率,Cμ=0.085.
模型(xíng)邊界條件包括速(sù)度人口、壓力出口(kǒu)、無滑移壁面邊界(jie),在近壁面區域采(cǎi)用标準壁面麗數(shu)進行處理.采用軸(zhóu)對稱💚邊界,即模型(xing)對稱軸的徑向速(su)度爲0.在求解離散(san)方程組和壓力速(sù)度耦合時選擇了(le)SIM-PLE算法,動量和湍流(liú)動能分别采用的(de)是二階迎風與一(yi)階迎風差分格式(shì).
2.2仿真文收
利用孔(kong)闆模型的軸對稱(cheng)性的特征,在圓柱(zhù)坐标系😍下建立它(ta)♌們的1/2實體模型,取(qǔ)壓方式采用D-D/2取壓(ya)其計算域⚽如圖❤️1所(suo)示.孔闆.上遊直管(guǎn)段長度爲20D,充足的(de)上遊管長能夠确(que)保液流在孔闆上(shàng)遊爲充分發展的(de)湍流流動.模型具(ju)體尺寸,其中D=12.3mm,β=0.247,Lu=246mm,Lt=494mm,t=2mm.
爲了(le)表現孔闆前後的(de)流場變化情況,首(shou)先在壁面🏃🏻♂️附近劃(huà)分邊界層網格,邊(bian)界層第一次厚度(du)爲0.1mm,共10層☎️,高度增長(zhang)因子1.1.其次,爲了😄提(ti)高孔闆附近的計(ji)算精度,對靠近孔(kong)闆部分的網格進(jìn)行局部加密,離節(jie)流孔越遠,網💚格越(yuè)稀疏最後,利用結(jie)構化網格生成方(fāng)📧式劃分其餘部分(fen)網格.
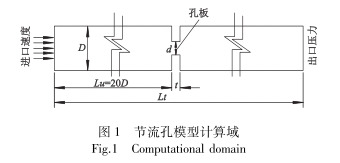
文中所選用(yong)的流體介質爲常(cháng)溫狀态下的水.人(rén)口流✔️速設定爲某(mou)一-頻率下的正弦(xian)流動u=uarg+uamp·sin(2πƒt),選擇不同平(ping)均流速uarg、流速振幅(fú)uamp和振蕩🌂頻率ƒ參數(shù)作爲節流孔的人(ren)口流速,具體參數(shù)見表1.利用UDF功能将(jiāng)該自定義速⛷️度函(hán)數加載在模型的(de)速度人口.
3網出第(dì)日
3.1振蕩差絡
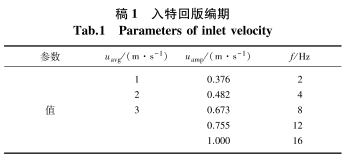
通過(guò)後處理後可以觀(guan)察到,當人口流速(sù)爲某一頻率下的(de)正🌏弦流動時,孔闆(pǎn)兩端将出現與人(ren)口流速頻率❄️相同(tóng)的振蕩差壓.如圖(tu)2所示,節流孔瞬時(shí)流量與差壓🌍振蕩(dang)頻❌率相等且具有(yǒu)固定的🤩相位滞後(hou).相位滞後意味着(zhe)測量壓差不能反(fan)映當時的流量情(qíng)👉況.此外,由于壓差(chà)測量裝置的動作(zuò)時限,測量壓差🔴滞(zhi)後,不能及時反映(yìng)瞬時壓差的變化(hua)因此,在📐振蕩流态(tai)下,孔闆流量計對(dui)瞬🛀🏻時流量的測量(liang)存在不确♍定性.
圖(tú)3爲人口流速振幅(fu)與差壓幅值的關(guan)系.對于同一振⭐蕩(dàng)頻率的入口流速(su),孔闆兩端差壓幅(fú)值随人口流速振(zhèn)幅💯增大而線性增(zeng)大,但其線性增長(zhǎng)系數與振蕩頻率(lü)有關🙇🏻.
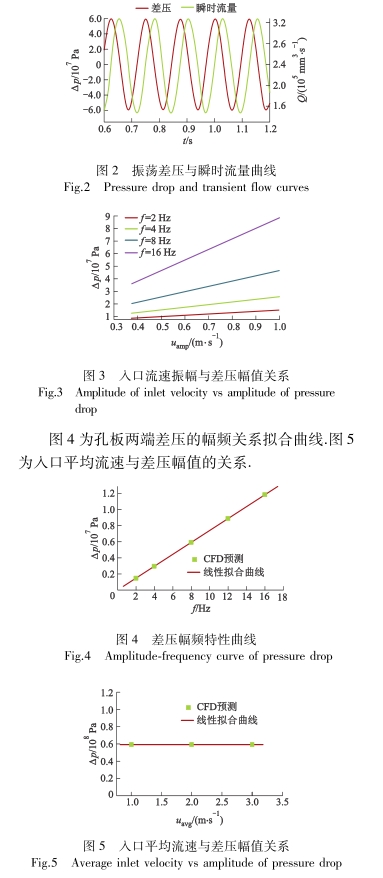
從圖4中可以(yi)看出當人口流速(su)振幅一定時,節流(liú)孔兩端差壓🔴的⭕振(zhèn)蕩幅值随振蕩頻(pin)率的增大而增大(da)♉.差壓💚幅值與振㊙️蕩(dang)頻率存🐅在近似一(yi)次線性關系.
在孔(kǒng)口恒定出流情況(kuàng)下,測量流量與實(shí)際節流孔流💁量Qv相(xiàng)同.而在振蕩流态(tai)下,差壓幅值随振(zhen)蕩頻率🐆線性增大(da),則測量流量幅值(zhí)越大,與實際節流(liú)孔流量的偏差也(yě)越大.
從圖5中可以(yi)看出,平均入口流(liu)速的變化,對壓力(lì)幅🔞值的影響幾乎(hū)可以忽略.
3.2瞬時流(liu)量差
在振蕩流态(tài)下,孔闆前後回流(liú)區和旋渦域的大(da)小随人口流速變(biàn)化不斷改變,導緻(zhì)進出口流量存在(zài)㊙️.瞬時流量差△Q,如圖(tu)6所示.瞬時流量差(chà)表現爲複雜的周(zhou)期性波動,其波動(dòng)周期與差壓振蕩(dàng)周期相同,相位介(jie)于瞬時流量和差(cha)壓兩者之間,且稍(shāo)滞後于振蕩差壓(yā).當差壓增大至峰(feng)值點時,瞬時❗流量(liàng)差趨向其波峰,并(bing)在到達峰值點後(hòu)反向階躍.
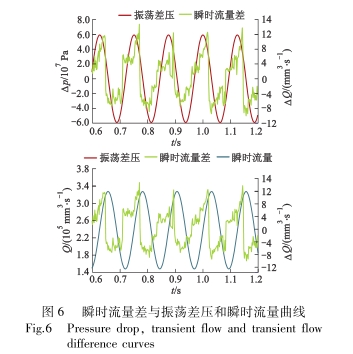
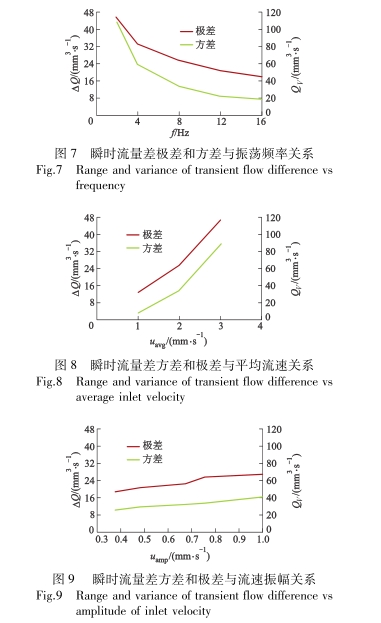
爲研究(jiū)人口流速各參數(shu)對瞬時流量差的(de)波動特性影響,對(duì)仿真記錄的瞬時(shí)流量差數據作方(fang)差分析和極差分(fèn)析,以此💜描述🔞瞬時(shí)流量差的波動情(qíng)況.瞬時流量差的(de)🏒極差和方差與振(zhèn)蕩頻率關系如圖(tu)💯7所示.當入口平均(jun1)流速和流速🆚振幅(fú)不變時,瞬時流🈲量(liang)差的極差和方差(cha)随人口流速的振(zhèn)蕩頻率增大而減(jiǎn)小也即人口流速(sù)頻率越大,瞬時流(liú)量差‼️的波動程度(du)越小,同時波動的(de)峰值也越小.
圖8爲(wei)入口平均流速與(yǔ)瞬時流量方差及(ji)極差的關系.當振(zhèn)蕩頻率和流速振(zhen)幅相同時,人口平(ping)均流速越大,瞬時(shi)流量✂️差的方差和(he)極差越大.圖9爲瞬(shun)時流量差方差和(hé)極差與流速振幅(fu)㊙️關系.從圖中可以(yǐ)看出,當人口平均(jun)流速相同時,對于(yú)給定的振蕩頻率(lü)☔,瞬時流量差🔞的方(fang)差和極差随着流(liú)速振幅增大而增(zēng)大.因此,當人口流(liu)速峰值越大,瞬時(shi)流量差波動也越(yue)大,瞬時流量差就(jiù)越⭕不穩定.
4結論
當(dāng)孔闆流量計所計(jì)量不可壓縮流體(tǐ)爲低頻振蕩流動(dong)狀态時,通過前述(shu)CFD分析,得到如下結(jié)論:
1)孔闆兩端差壓(yā)爲周期振蕩狀态(tai),差壓與節流孔瞬(shùn)時流量同頻不同(tong)相.差壓幅值随人(rén)口流速振幅增大(da)而線性增大,且線(xiàn)性增長系數與振(zhèn)蕩頻率相關.
2)圓管(guan)人口與出口存在(zài)周期波動的瞬時(shí)流量差,振🌂蕩頻率(lǜ)越大或人口流速(sù)峰值越小,則瞬時(shi)流量差的波動也(yě)越小
3)在振蕩流态(tài)下,由于相位滞後(hòu)和瞬時流量差的(de)存⛹🏻♀️在🔱,使孔闆流量(liàng)計的測量流量與(yǔ)實際出口流量之(zhi)✂️間存在偏差振蕩(dang)頻率越大,偏差也(ye)越大..
4)孔闆流量計(ji)作爲的流量計量(liang)的常用元件,該分(fen)析結果對孔闆的(de)結構設計及系統(tǒng)的整體動态特性(xìng)研究具有重要意(yi)義. 本文來源于網(wang)絡,如有侵權聯系(xì)即删除!