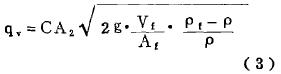在使用轉(zhuǎn)子流量計(jì) 的實際工(gōng)作中常會(hui)用到工作(zuo)原理公式(shi)。然而目前(qián)不少文獻(xian)對該公式(shì)的推導過(guo)程存在二(èr)些原則性(xìng)的缺欠,爲(wei)便于💃🏻正确(que)理解和使(shi)用轉子流(liú)量計工作(zuò)原理公式(shi),對此🔴提出(chu)一些商榷(què)性意見,供(gòng)參考。
　　對于(yú)轉子流量(liang)計工作原(yuán)理公式的(de)推導,查閱(yue)國内外的(de)文獻資料(liào)其方法基(ji)本相同。現(xiàn)簡述如下(xià):
首先根據(jù)Bernolltil方程導得(dé)節流裝置(zhì)的體積流(liu)量表達式(shi)🤟:

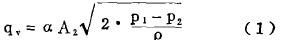
然後根據(ju)轉子受力(lì)的平衡式(shì)
（P1-P2）Af=Vfg(ρf-ρ)　　　　　　(2)
把(2)式代入(rù)(1)式并考慮(lü)轉子流量(liàng)計的實際(ji)流動中的(de)阻力得:

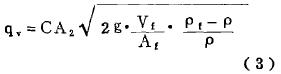
　　該(gai)(3)式即爲轉(zhuan)子流量計(jì)的工作原(yuán)理公式。雖(sui)然(3)式在實(shi)際🌈使🤞用中(zhong)⛷️正确無誤(wù),但其推導(dǎo)過程中的(de)(2)式有錯誤(wu),在未加任(rèn)何假定的(de)條件下(2)式(shì)不成立(參(can)考文獻都(dōu)未加任何(he)說🈚明)。對于(yu)(3)式在實🌍際(jì)使用中雖(suī)能正确無(wu)誤,但這是(shì)由于轉🌐子(zǐ)流量計🐉流(liu)量系數C是(shi)通過實驗(yan)測定的緣(yuan)😘故,從而遮(zhē)蓋了(2)式的(de)錯誤。
　　對(2)式(shi)進行分析(xi),不難看出(chu)它表示轉(zhuǎn)子所受向(xiàng)上爲力❄️p1Af與(yu)所受向下(xia)的力p2Af之差(chà)等于轉子(zǐ)在流體中(zhōng)的向下重(zhong)力,使轉子(zi)處于相對(dui)靜止平衡(heng)狀态。但是(shi)錯誤發生(sheng)在對由壓(yā)💘強所引起(qǐ)的向上力(li)p1Af的處理方(fāng)法上🚶。由壓(ya)強引起的(de)向上⁉️力在(zai)不加任何(he)說明的情(qíng)況下不應(ying)該等于p1Af。

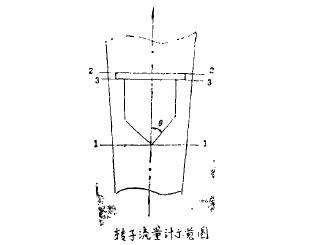
　　轉(zhuan)子所受由(you)壓強引起(qi)的向上力(lì)包括兩部(bù)分,(見圖)。一(yi)部分在轉(zhuǎn)子的錐形(xing)部分,一部(bù)分是在3-3位(wei)置的轉子(zi)凸部位。轉(zhuan)子🐅的錐✊形(xíng)部❌分由于(yu)其環隙通(tong)道截面積(ji)的變化,壓(yā)強随之位(wèi)置而變化(huà),因此錐部(bù)表面積S所(suo)受壓強是(shi)不均勻的(de)。其所受向(xiang)上力應爲(wei):

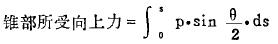
若以平均(jun)壓強pm,表示(shì)錐部所受(shòu)壓強,則上(shang)式可改寫(xiě)爲🌈:

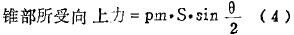
至于3-3位(wei)置轉子所(suǒ)受向上力(li)可由下式(shì)表示:

　　但對(dui)力的分析(xī)比較合理(lǐ),避免了像(xiàng)(2)式那樣不(bu)加任何說(shuo)明的原則(zé)性均缺欠(qiàn)。讀者在閱(yuè)讀其它文(wén)獻時應對(dui)♍此有一個(gè)清晰的認(ren)識,.以便在(zai)實際工作(zuò)中正确的(de)使用轉子(zǐ)👨‍❤️‍👨流量計工(gong)作原理公(gong)式。
符号說(shuo)明
A2轉子頂(ding)部2-2面位置(zhì)的通道截(jié)面積,m2
P1轉子(zǐ)下尖1一1面(miàn)位置的壓(ya)強〔Pa〕
P2轉子頂(ding)部2一2面位(wei)置均壓強(qiang)〔Pa〕
ρ流體密度(du)kg/m3
α由Bernoulli方程導(dǎo)出(1)式的校(xiao)正系數
C轉(zhuǎn)子流量計(jì)的流量系(xì)數
Af轉子的(de)最大部分(fen)的截面積(jī)m2
Vf轉子的體(ti)積m3
g重力加(jiā)速度m/s2
ρf轉子(zi)的密度kg/m3
ρ流(liu)體的密度(du)kg/m3
ρv流體均體(ti)積流量m3/S
P壓(yā)強〔Pa〕
pm轉子流(liu)量計錐部(bù)所受平均(jun1)壓強〔Pa〕
S轉子(zǐ)錐部的表(biǎo)面積m2
D轉子(zi)頂部的直(zhí)徑m
D 轉子中(zhong)部的直徑(jìng)m

以上内容(rong)來源于網(wang)絡，如有侵(qīn)權請聯系(xì)即删除!