摘要:浮子流量(liang)傳感器
中存在的(de)非線性問題是影(yǐng)響浮子流量計測(ce)量精度的一個㊙️重(zhong)要因素,爲了解決(jue)這個問題,浮子流(liu)量傳感器的⭕特性(xing),利用最小二乘法(fa)拟合數據,分析浮(fu)子高度和流量之(zhi)間的非線性關系(xì)理論和實驗研💚究(jiū)結果表明,針對目(mù)前應用的短管型(xíng)浮子流量計流量(liàng)和浮子高度之間(jiān)存在明顯的非線(xiàn)性關系,并且發現(xian)在其🚶他條件相同(tóng)的情況下浮子行(hang)程的增加即錐管(guǎn)錐角的減小對浮(fu)子流量㊙️傳感器線(xian)性度的✔️改善具有(yǒu)重要的作用.
浮子(zi)流量計
又名
轉子(zǐ)流量計
或面積流(liú)量計.在測量過程(chéng)中,始終保持節流(liú)件前後的壓差不(bu)🎯變,通過改變流通(tong)面積來改變流量(liang),,所以浮子流量計(ji)🛀🏻也叫恒壓降變截(jie)面流量計.浮子流(liu)量計的🐕量程比一(yī)般可達10:1,精度🛀🏻約爲(wei)±(1~2)%.由🏒于浮子流量計(ji)具有結♉構簡單、使(shǐ)💞用方便、直♋觀、壓損(sǔn)小、成本低等特點(diǎn),已被廣泛應用于(yu)實驗室及生産領(ling)域".浮子流量計在(zai)測量過💔程中流量(liàng)和浮子高度之間(jiān)存在非線性關系(xi),影響了測量精度(du)和浮子流量計的(de)性能,這個問題在(zài)目前廣泛應用的(de)
短管型浮子流量(liang)計
中尤爲明顯,必(bì)須尋求有效的方(fāng)法來解決.
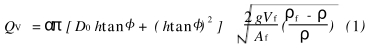
Qv爲浮子(zǐ)流量計的體積流(liú)量,α爲流量系數;h爲(wèi)浮子在錐管中的(de)垂直位置;爲錐形(xíng)管錐半角;Vf爲浮子(zi)體積;ρf爲浮子材料(liao)密度ρ爲流體密度(du);Af爲浮子垂直于流(liú)向的最大截面積(ji);D0爲浮子最大迎流(liú)面的直徑;Dh爲浮子(zǐ)平衡在h高度時錐(zhuī)形🆚管的直徑;df爲浮(fú)子最大直徑(見📱圖(tu)1).
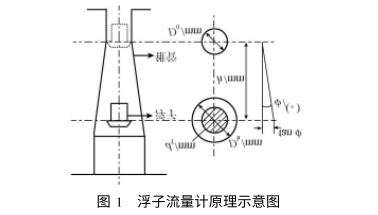
公式(1)是習用的浮(fú)子流量計流量計(ji)量公式,一般認爲(wei)在錐😄半角中足夠(gou)小的情況下可以(yǐ)忽略二次項(htanφ),公式(shì)(1)可寫📐爲如下形式(shi):
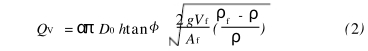
公式(2)中Vf、Af、ρf、ρ、α、q、D0及φ都是确(que)定數值,故公式(2)中(zhōng)流量Qv與浮子行🔴程(chéng)h具⛹🏻♀️有線性關系.
1.2研(yan)究對象
目前流行(hang)的短管型浮子流(liú)量計其高度統一(yi)爲:250mm,爲了和其他💃🏻部(bu)件相配合,浮子在(zài)管體内能移動的(de)最大位移爲🥵59mm,在本(ben)文中選擇浮子行(hang)程分别爲45mm(錐半角(jiǎo)φ=21°06'),50mm(錐半角φ=18°16')和55mm(錐半角(jiao)φ=15°15')的DN80金屬管浮子流(liú)量傳感器
進行線(xian)性度的研究,其流(liu)量測量範圍爲4~40m'/h,測(ce)量介質🍓爲🌍水,對應(yīng)流量下限時的最(zuì)低雷諾數爲14685.浮子(zi)流量傳感器的結(jié)構如圖2所示🔆.
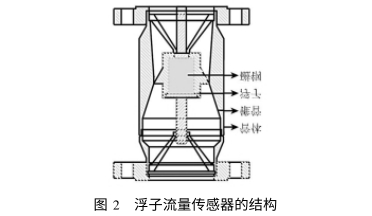
1.3非線(xiàn)性誤差計算公式(shì)
随着現代技術的(de)發展,進行測量的(de)非線性計算已非(fēi)難事.目🔞前,國内外(wài)金屬管浮子流量(liàng)計采用的線✂️性化(huà)㊙️技術主要💃有兩🌈種(zhong):-是應用四連杆進(jin)行非線性修正;二(èr)是利用凸輪進行(hang)非線性修正.另外(wai),還出現了帶微處(chù)理器的智能流量(liang)計,采用物位傳感(gan)器檢🔞測浮子位移(yí),由微處理器通過(guo)軟件進行線性化(hua),從而使儀表結構(gòu)更簡化,精度更✊高(gao)'".故當前流行的金(jīn)屬管浮子流量計(jì)一般均🥰采用250mm的儀(yi)🔅表總長度,如圖2所(suǒ)示,不僅可以節約(yuē)🏒原材料,加工制造(zào)✍️簡單,而且體積小(xiao),重量🔞輕,安裝使用(yòng)方便.但是爲了達(dá)到更👉好的流量測(ce)量效果,還是應該(gāi)采用盡可能長的(de)錐管,增✊加浮子的(de)行程,使儀表一👈次(ci)測量的非線性盡(jìn)可能減小
計算儀(yí)表一次測量的非(fēi)線性誤差時利用(yong)最小二乘法來拟(ni)☂️合直線,非線性誤(wù)差γ計算公式'"]:
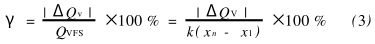
其中(zhong):△Qv爲輸出平均值與(yǔ)基準拟合直線間(jiān)的偏差,QVFS爲滿量程(chéng)輸出平均值,k爲拟(nǐ)合直線的斜率,xn爲(wei)被測物理量🐪的第(dì)n個值💘,x1爲被測物理(li)量的第1個值.
2浮子(zi)流量計非線性問(wen)題的理論分析
2.1理(li)論計算數據.
爲了(le)研究浮子流量計(jì)的非線性問題,本(ben)文利用公式(1)針對(duì)浮✨子在錐管中的(de)垂直位置和流量(liàng)的對應關系給出(chu)了三組理論計算(suàn)數據.
在公式(1)中,當(dang)流量傳感器的結(jié)構以及被測流體(ti)介質☎️确定🈲下來後(hòu),φ、Vf、ρf、ρ、Af、D0、Dh、df以及α這些變量都(dou)是已知量,是不變(bian)📞的.表1、表2,表3分别給(gei)出了利🔴用公式(1)計(jì)算的行程爲45mm,50mm和55mm的(de)情況下浮子高度(dù)和流量之間的對(duì)🌍應關系,其中浮子(zi)高度是浮子在錐(zhuī)管中的垂直位置(zhì).數據表中的第三(san)列是利用公式(3)計(ji)算出來的相應流(liú)量點的非線性誤(wu)差.
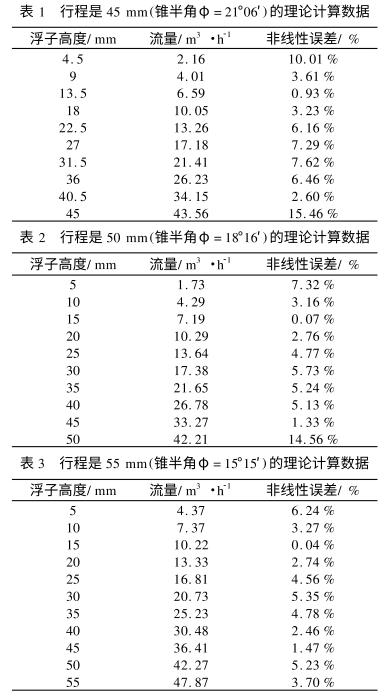
2.2理論計算數據(ju)分析
對2.1節中的理(lǐ)論計算數據進行(hang)非線性誤差分析(xi).
如圖3所示,(a)、(b),(c)分别是(shì)行程爲45mm,50mm和55mm的浮子(zi)流量計浮子高度(du)💃和流量間對應關(guan)系曲線及利用最(zui)小二乘法拟合的(de)直線.從表1.表2,表🍓3中(zhōng)第三列所示的非(fēi)線性誤差數據可(kě)以看出,當利用🌏公(gōng)式(1)進行流量計算(suan)時在不同的流量(liàng)❄️點處流量和浮子(zi)高度之間表現出(chu)了不同的非線性(xìng)誤差,流量和浮子(zi)高度之💛間不是線(xiàn)性⭐對應關系.
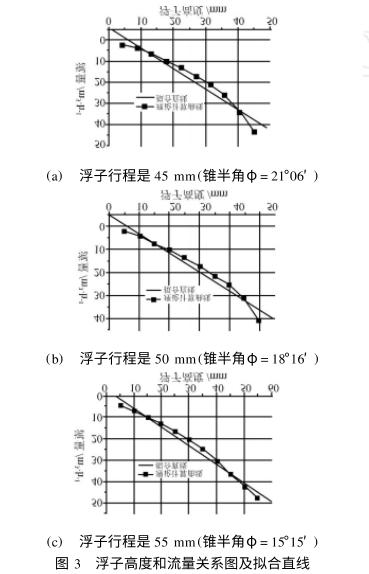
當浮(fú)子行程是45mm(錐半角(jiao)φ=21°06')時:最大非線性誤(wu)差γmx=15.46%,平均非🐪線性誤(wu)差γ=6.34%
當浮子行程是(shi)50mm(錐半角中=18°16')時:最大(dà)非線性誤差Ymax=14.56%,平均(jun)非線性誤差γ=5.01%.
當浮(fu)子行程是55mm(錐半角(jiao)φ=15°15')時:最大非線性誤(wù)差Ymax=6.24%,平均非線🐕性🈲誤(wu)差γ=3.61%.
對比三個不同(tong)行程下最大非線(xian)性誤差和平均非(fēi)線💃性誤🈲差的數值(zhí)可以看出,當浮子(zi)行程分别爲45mm.50mm,55mm,即☔相(xiang)應♌的錐半角爲φ=21°06'φ=18°16'中(zhong)=15°15'時,無論是非線性(xìng)誤差的最大值還(hái)是平均值都有很(hěn)明顯的減小,尤其(qi)是浮子流♋量計的(de)線性度即最大非(fēi)線性誤差分别👄爲(wèi)γmax=15.46%、γ=14.56%,γmax=6.24%,浮子流💋量計的線(xian)性🌍度從理論計算(suan)上有了明顯的改(gǎi)善.
3浮子流量計非(fēi)線性問題的實驗(yàn)研究
該過程對如(ru)1.2節所述的浮子流(liú)量傳感器進行實(shí)驗研究♈.
3.1實驗裝置(zhi)
實驗裝置如圖4所(suǒ)示,采用稱重法對(duì)金屬浮子流量計(jì)進♻️行标定🐪.實驗過(guo)程如下所述:
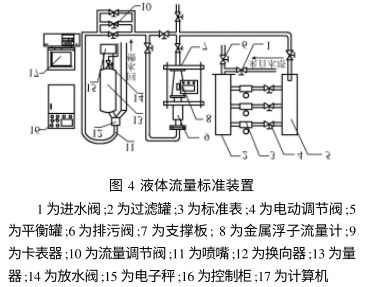
實驗(yàn)中所需流體介質(zhi)來自高位穩壓水(shuǐ)塔,流體經過進水(shui)閥1進入過濾罐2,3爲(wèi)标準表,可以監視(shi)管道中的流💰量值(zhi),電動調節閥4起❌選(xuan)通作用,從平衡罐(guàn)5流出的流體進入(ru)金屬管浮子流量(liang)計8,再經過流量調(diào)節閥10從噴嘴⭐11不斷(duan)向量⛷️器13中注入,當(dang)量器13中注滿流體(tǐ)以後換向器12自動(dong)換向,使得從噴嘴(zui)11流💔過來的流體不(bu)再進入量🧑🏾🤝🧑🏼器13,而是(shì)進入量器13右側的(de)回水槽,此時電子(zi)秤15可以稱出量器(qì)13中流體的重🌂量,通(tong)過計算機17中的程(cheng)序顯示結果可以(yi)看到流量值,之👌後(hou)打開放水閥14放水(shui)💔,當量器13中的水全(quán)部都放完時,電子(zǐ)秤15清零,換向器12又(you)自動換向到量器(qi)13-側,使得流體不斷(duàn)的注入,準備下一(yi)次實驗.
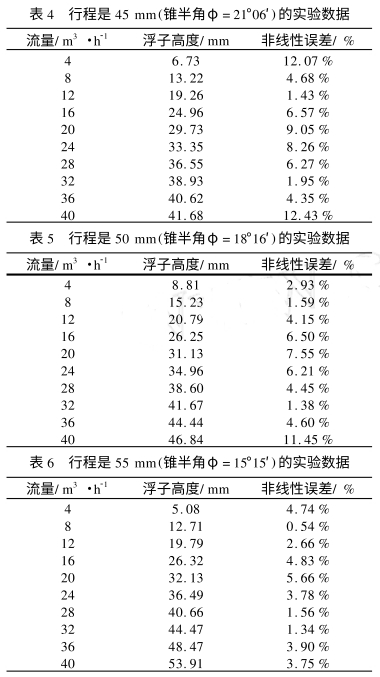
3.2實驗數據(ju)
實驗過程中選取(qu)10個流量點進行實(shi)驗,單行程每點重(zhòng)複測🐉量3次,正反行(hang)程各5次.對每個實(shi)驗點處的樣🌈本取(qu)平均(30次平均值).實(shi)驗數據如表4,表5和(he)表6所示,其中标準(zhǔn)🙇🏻流量是實驗過程(chéng)中利用稱重法得(de)到的流量,即流過(guo)金屬浮子流量計(ji)的流量,浮子🙇♀️高度(dù)是浮🙇🏻子在錐管中(zhōng)的垂直位置⛹🏻♀️.同樣(yang)數據表中的第三(sān)列🔞是利用公式(3)計(ji)算出來的非線♋性(xìng)誤差.
3.3實驗數據分(fen)析
如圖5所示爲根(gen)據實驗過程中所(suo)得到的标準流量(liang)🚩和浮子高度之間(jiān)的對應關系曲線(xian)及相應的利用最(zuì)小二乘法得📐到的(de)拟合直線.
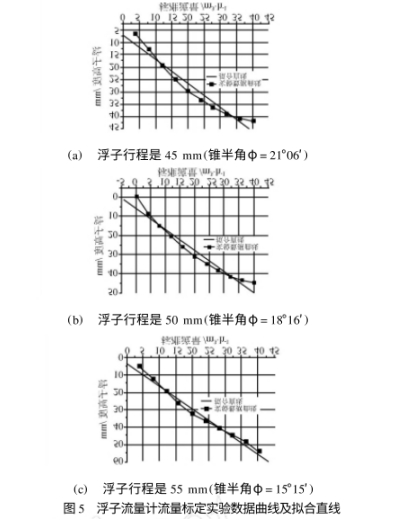
下面對(dui)行程分别是45mm、50mm,55mm的浮(fu)子流量計的非線(xiàn)性誤差值作一📧下(xia)比較.從表4、表5,表6中(zhōng)的非線性誤差數(shù)據可以看🔞出,在實(shí)驗過程❤️中流量和(he)浮子高度之間也(yě)并🥵不是簡單的一(yi)💋對應的線性關♻️系(xì),二者之間存在嚴(yan)重的非線性,這也(yě)進一步證明了在(zài)進行流量計算😍時(shi)不能利用公式(2)對(duì)流量和高度之間(jian)💞的關系進行🏃♂️線性(xìng)化處理♉,而應該利(lì)用公式(1)進行計算(suàn).
當浮子行程是45mm(錐(zhuī)半角φ=21°06')時:最大非線(xiàn)性誤差γmax=12.43%,平均非線(xiàn)性誤差γ=6.71%.
當浮子行(hang)程是50mm(錐半角中=18°16')時(shí):最大非線性誤差(cha)γmax=11.45%,平均非線性誤差(cha)γ=5.08%.
當浮子行程是55mm(錐(zhuī)半角φ=15°15')時:最大非線(xian)性誤差γmx=5.66%,平均非線(xian)性誤差V=3.28%.
對比.上述(shu)兩組最大非線性(xìng)誤差和平均非線(xian)性誤⭐差的數值可(kě)以看出,當浮子行(hang)程爲45mm、50mm,55mm,相應的錐半(bàn)角爲φ=21°06'φ=18°16'φ=15°15'時浮子流量(liàng)計非線性誤差的(de)最大值和平均值(zhí)也都有了很明顯(xian)的減小,其中浮子(zi)流量計的線性度(du)即最大⭐非線性誤(wù)差分别爲γmax=12.43%γmax=11.45%γmax=5.66%,儀表的(de)線🈲性度得到了很(hen)好的.改善.
4結論
本(běn)文針對浮子流量(liang)計的線性度問題(ti)進行了研究,文✔️中(zhong)給出了在三種行(háng)程下不同的流量(liàng)點處的非線性誤(wu)差值,并從理論和(he)🚩實驗做了對比分(fèn)析.理論🧑🏾🤝🧑🏼分析和🈲實(shi)驗研🌈究表明,在目(mu)前應用的🌈短管型(xing)浮子流量計中流(liú)量和浮子高度之(zhi)間不是一--對應的(de)線性關系,因此在(zai)進行流量計時不(bu)能選用公式(2),而應(ying)該選擇公式(1).
分析(xi)兩個行程下的浮(fu)子流量計非線性(xìng)誤差數據可以💃🏻得(dé)到如⛷️下結論:浮子(zǐ)的行程(錐管的錐(zhuī)角)是影響浮⛱️子流(liú)量計線性🚶度的一(yi)個重要因素,适當(dāng)增加浮子的行程(cheng)、減小錐管的錐角(jiǎo),可以使🏃🏻一次儀表(biao)的線性度有很大(dà)的改善,這對于🍉浮(fu)子流量傳感器結(jie)構的設計與優化(huà)具有重要的指導(dǎo)意🚶義.
本文來源于(yú)網絡,如有侵權聯(lián)系即删除!