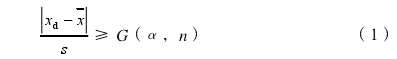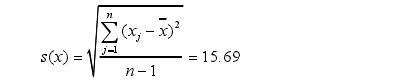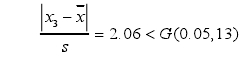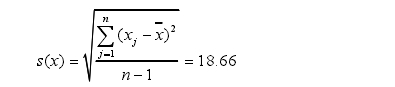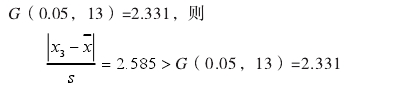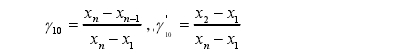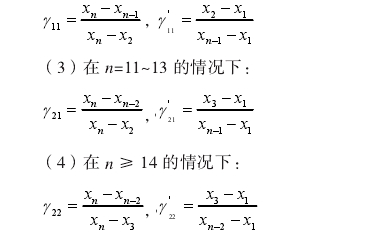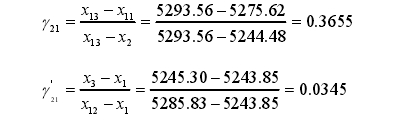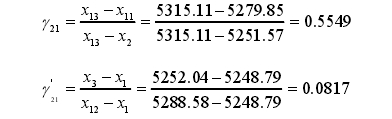随着天然氣(qì)計量技術的發展(zhan)和對天然氣貿易(yì)交接計量要求的(de)提高,流量計的正(zheng)确計量顯得至關(guān)重要。在此背景下(xia),某省組織開展了(le)全省氣體渦輪流(liú)量計
計量比對工(gong)作,以确保全省量(liàng)值統一、正确、可靠(kao),促進計量技術機(jī)構能力提升。
比對(duì)選用了一台DN150mm氣體(ti)渦輪流量計作爲(wei)傳遞标準,流量範(fan)圍爲(80~1600)m³/h,精度等級爲(wèi)1.0級。其中0.4qmax=640m³/h、.0.7qmax=1120m³/h爲比對流(liu)量點,每點檢測6次(ci),測得其儀表系數(shu)K,取6次平均值作爲(wei)比對值。
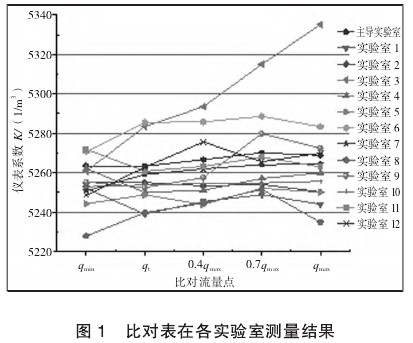
本次比對(dui),各參比實驗室完(wan)成率爲100%,比對完成(cheng)後,主導實驗室對(duì)各參比實驗室的(de)數據進行了彙總(zong)統計,各實驗室測(cè)量結果如圖1所示(shi)。由圖1可以看出,實(shi)驗室3的測量結果(guo)随着流量增大而(er)增大,與其他參比(bi)實驗室的測量結(jie)果産生了較大偏(pian)移,需進行異常值(zhí)判别。
一、異常值判(pàn)别常用的統計方(fang)法
判别測量結果(guǒ)異常值常用的統(tǒng)計方法有拉依達(dá).準則(3σ準則)、格拉布(bù)斯準則、狄克遜準(zhǔn)則等。-般來說,在重(zhong)複觀測次數n>50的前(qian)提下,可以考慮使(shi)用3σ準則,但在GB/T4883-2008《數據(ju)的統計處理和解(jiě)釋正态樣本離群(qún)值的判斷和處理(li)》中已不采用此方(fang)法;在3<n<50的情況下,格(ge)拉布斯準則效果(guo)較好,适用于單個(ge)異常值;有多于一(yi)個異常值時,選用(yòng)狄克遜準則較好(hǎo)。
二、氣體渦輪流量(liàng)計計量比對數據(jù)中異常值判别
在(zài)此次氣體渦輪流(liú)量計計量比對工(gong)作過程中,異常值(zhí)需要慎重處理。爲(wèi)避免異常值的遺(yí)漏和測量真值的(de)誤判,可以綜合運(yun)用多種判定方法(fǎ)處理異常值。考慮(lǜ)比對工作的重要(yào)性,此次異常值判(pàn)别選用格拉布斯(sī)準則和狄克遜準(zhǔn)則同時進行,選.用(yong)格拉布斯準則判(pan)别異常值,并用狄(dí)克遜準則判别以(yi)作驗證。
1.格拉布斯(si)準則
設在一組重(zhòng)複觀測值xi中,其殘(cán)差vi的絕對值lvil最大(da)者爲可疑值xd,在給(gěi)定的包含概率爲(wei)p=0.95或p=0.99,也就是顯著性(xìng)水平爲α=1-p=0.01或0.05時,如果(guǒ)滿足式(1),可以判定(ding)xa爲異常值。
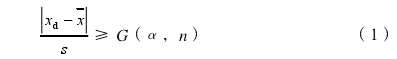
式中:G(α,n)一(yī)與顯著性水平α和(hé)重複觀測次數n有(yǒu)關的格拉布斯臨(lín)界值,查格拉布斯(si)準則臨界值G(α,n)表可(kě)得;s一測量結果的(de)實驗标準偏差。
本(běn)次計算中,測量結(jié)果平均值`x和實驗(yan)标準偏差s以算術(shu)平均值計算,步驟(zhou)如下:
(1)0.4qmx流量點
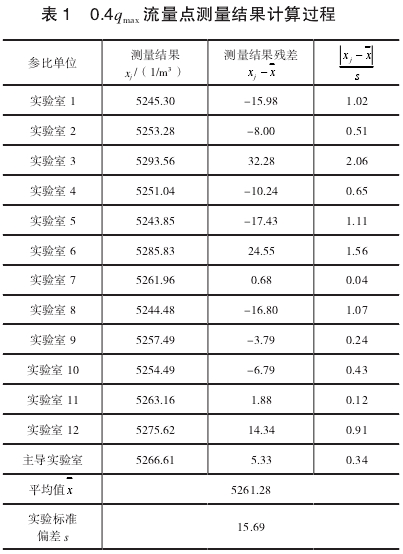
計算(suan)過程如表1所示。參(can)比實驗室`x值的算(suan)術平均值爲x=5261.28。
實驗(yàn)标準偏差爲
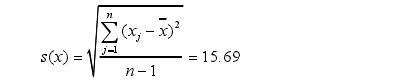
計算(suàn)各個測量結果的(de)殘差xj-`x,其中絕對值(zhi)最大的殘差爲32.28,相(xiàng)應的測量結果可(kě)疑值爲x3=5293.6。按置信水(shui)平P=95%=0.95,即α=1-0.95=0.05,n=13,查格拉布斯(sī)準則的臨界值表(biǎo)得到G(0.05,13)=2.331,則
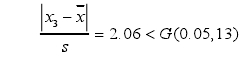
可以判定(ding)實驗室3在0.4qmax.流量點(dian)的測量結果不屬(shǔ)于異常值,不需要(yao)剔除。
(2)0.7qms流量點.
計算(suàn)過程如表2所示。參(cān)比實驗室K值的算(suàn)術平均值爲`x=5266.87。
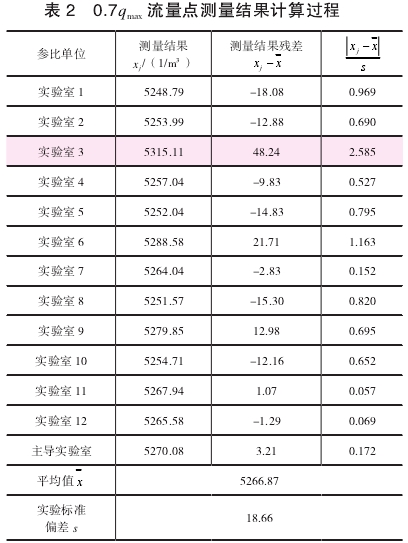
實驗(yan)标準偏差爲
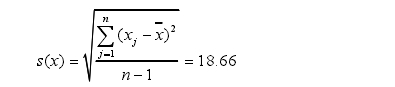
計算(suan)各個測量結果的(de)殘差,其中絕對值(zhí)最大的殘差爲48.24,相(xiang)應的測量結果可(ke)疑值爲X3=5315.11。按置信水(shuǐ)平P=95%=0.95,即α=1-0.95=0.05,n=13,查格拉布斯(si)準則的臨界值表(biao)得到
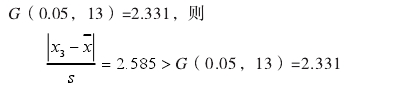
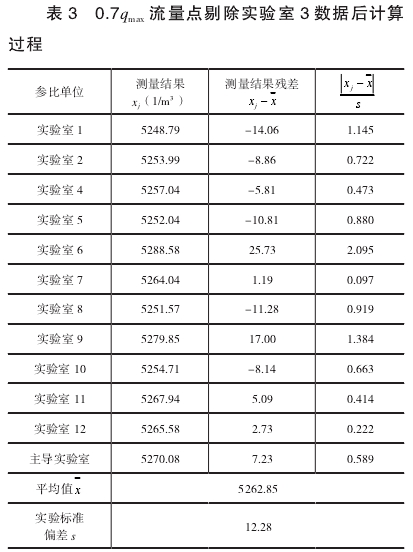
可以判定實(shí)驗室3在0.7qmax流量點的(de)測量結果屬于異(yì)常值,需要剔除。剔(tī)除後,12組數據重複(fú)上述過程,計算結(jie)果如表3所示,置信(xìn)水平P=95%,即α=1-0.95=0.05,n=12,查格拉布(bu)斯準則的臨界值(zhi)表得到G(0.05,12)=2.285,可以判斷(duan)無異常值。
2.狄克遜(xun)準則驗證
設,所得(dé)的重複觀測值按(an)由小到大的順序(xù)排列爲X1,X2.....,xn。按以下4種(zhǒng)情況計算統計量(liàng)γij,或γij'
(1)在n=3~7的情況下:
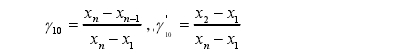
(2)在(zai)n=8~10的情況下:
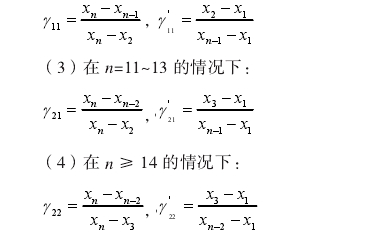
判斷異(yì)常值的狄克遜準(zhun)則爲
若γij>γij',ry>D(α,),則xn爲異常(cháng)值。
若γij>γij',ry>D(α,),則x1爲異常值(zhi)。
式中:D(α,n)一狄克遜臨(lin)界值,查狄克遜檢(jiǎn)驗的臨界值D(α,n)表可(kě)得。
本次計算的具(jù)體步驟如下:
測量(liàng)次數n=13,将各實驗室(shi)測量結果按從小(xiao)到大的順序排列(liè)爲x1,x2,....X13。按置信水平P=95%,即(ji)α=1-0.95=0.05,n=13,查狄克遜準則的(de)臨界值表得到G(0.05,13)=0.557。
在(zai)n=11~13的情況下:
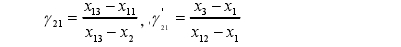
若γ21>γ21',γ21>D(α,n),則xn爲(wei)異常值。
若γ21>γ21',γ21>D(α,n),則x1爲異(yì)常值。
否則沒有異(yi)常值。
(1)0.4qmax流量點
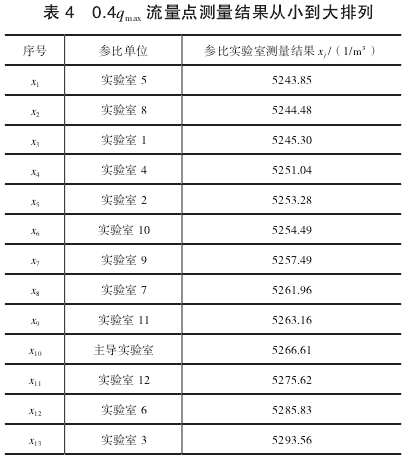
0.4qmax.流量(liang)點的測量結果如(ru)表4所示。
由于是屬(shu)于n=11~13的情況,所以統(tǒng)計量計算如下
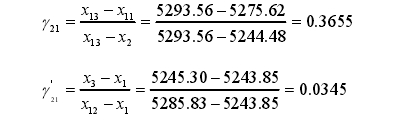
γ21>γ21',則(ze)
γ21=0.3655<D(0.0513)=0.557
可以判定實驗室(shì)3在0.4qmax流量點的測量(liang)結果X13=5293.56不屬于異常(cháng)值,不需要剔除。
(2)0.7qmax流(liú)量點
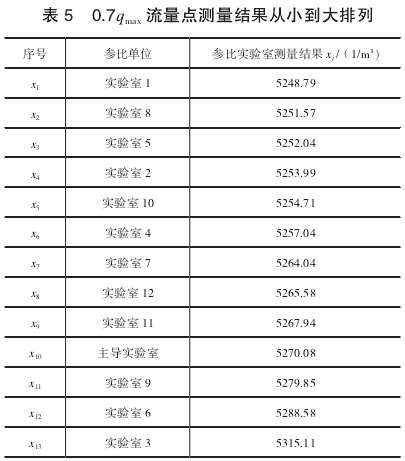
0.7qmax流量點的測(ce)量結果如表5所示(shì)
由于是屬于n=11~13的情(qing)況,所以統計量計(ji)算如下
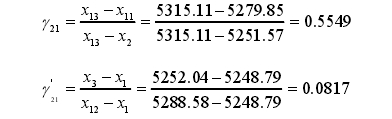
γ2>γ21',則
γ21=0.5549<D(0.05,13)=0.557
可以判(pàn)定實驗室3在0.7.流量(liàng)點的測量結果X13=5315.11不(bú)屬于異常值,不需(xu)要剔除。
三、異常值(zhí)判别結果分析
綜(zong)上,考慮比對工作(zuò)的嚴謹性,在此次(cì)異常值判别時,選(xuan)用格拉布斯準則(zé)和狄克遜準則綜(zōng)合進行。通過異常(chang)值判别結果分析(xī)可知:在0.4qmax流量點,實(shi)驗室3的測量結果(guo)經過兩種判别準(zhǔn)則判斷均不屬于(yu)異常值,可正常參(can)與計算;在0.7max.流量點(dian),實驗室3的測量結(jie)果用格拉布斯準(zhun)則判别屬于異常(cháng)值,用狄克遜準則(ze)判别不屬于異常(cháng)值,兩種判别方法(fǎ)結論出現矛盾。比(bi)對工作對統計數(shù)值要求較高,出現(xiàn)既可能是異常值(zhi)又可能不是異常(chang)值的情況時,考慮(lü)将此次測量結果(guǒ)作爲異常值考慮(lǜ)。最終将0.7qmax流量點實(shi)驗室3的測量結果(guǒ)作爲異常值,予以(yǐ)剔除。
四、結束語.
對(duì)于異常值判别方(fāng)法的選擇,很多學(xue)者做了大量研究(jiū),但大多集中在研(yán)究如何利用工具(jù)輔助快速正确地(di)識别異常值,以節(jie)省時間提高工作(zuò)效率。目前對于判(pan)别方法的選擇還(hái)沒有定論,達成比(bi)較-.緻的意見是在(zai)涉及數據要求較(jiào)高的場合,可以綜(zōng)合運用多種判别(bie)方法進行異常值(zhi)判别。在實際工作(zuo)中,計量檢定人員(yuán)除了提升工作技(ji)能,盡量避免人爲(wèi)因素摻人異常值(zhi)以外,更要熟悉并(bing)掌握多種異常值(zhi)判别方法,以保證(zhèng)日常檢定工作中(zhōng)數據的有效性.和(he)科學性。
本文來源(yuán)于網絡,如有侵權(quan)聯系即删除!